MOCK TEST - 1 - Quantitative Ability (QA Section)
Quantitative Ability is one of the section of CAT exam along with Data Interpretation and Logical Reasoning and Verbal Ability and Reading comprehension. Practice tests or Mock tests help aspirants to prepare for the exams.
Quantitative Ability is the ability of a person to make empirical enquiries through numerical data gathering and analysis by performing mathematical or statistical computations.
Maximum Time for this section: 40 : 00 (Minutes : Seconds)
Total number of Questions: 68
Total number of MCQ's Questions: 50
Total Number of Non-MCQ's (TITA) Questions: 18
Total number Quantitative Ability (QA) Questions: 22
Total number Quantitative Ability (QA) MCQ's Questions: 14
Total number Quantitative Ability (QA) non-MCQ's (TITA) Questions: 08
Total number Data Interpretation and Logical Reasoning (DILR) Questions: 20
Total number Data Interpretation and Logical Reasoning (DILR) MCQ's Questions: 15
Total number Data Interpretation and Logical Reasoning (DILR) non-MCQ's (TITA) Questions: 05
Total number Verbal Ability & Reading Comprehension (VARC) Questions: 26
Total number Verbal Ability & Reading Comprehension (VARC) MCQ's Questions: 21
Total number Verbal Ability & Reading Comprehension (VARC) non-MCQ's (TITA) Questions: 05
Maximum Time: 40 : 00 (Minutes : Seconds) per section
Note-1: Use of simple calculator is allowed.
Note-2: Not allowed to change section once selected.
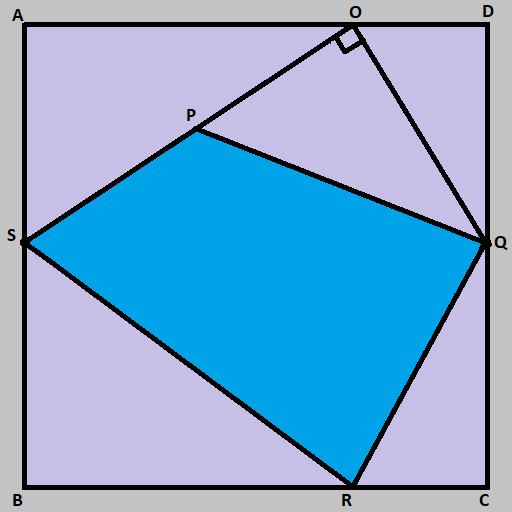
ABCD is a square ▢re of side 10 cm as shown in the figure. If AS is 6 cm, QC is 5 cm, OD is 3 cm, BR is 7 cm and P is the mid-point of the line SO, find the area of the quadrilateral PQRS.

Options:
Option (a): 36.5604 sq cm.
Option (b): 21 sq cm.
Option (c): 30.56sq cm.
Option (d): 29.06 sq cm.
Given:
AB = BC = CD = DA = 10 cm, AS = 6 cm, QC= 5cm, OD = 3cm, BR = 7 cm and P is the mid-point of SO.
Now,
SB = AB – AS = 10 - 6 = 4 cm.
RC = BC – BR = 10 - 7 = 3 cm.
DQ = CD – QC = 10 - 5 = 5 cm.
AO = DA – OD = 10 - 3 = 7 cm.
Area of the quadrilateral PQRS = Area of the Square ABCD ▢re - (Area of the Triangle ASO ▲le + Area of the Triangle POQ▲le + Area of the Triangle QRC ▲le + Area of the Triangle BSR ▲le + Area of the Triangle POQ ▲le)
Area of the Square ABCD with side a = a² = 10 x 10 = 100 sq cm.
Area of the Triangle ASO = 0.5 x AS x AO = 0.5 x 6 x 7 =21 sq cm.
Area of the Triangle QRC = 0.5 x QC x RC = 0.5 x 5 x 3 = 7.5 sq cm.
Area of the Triangle BSR = 0.5 x BS x BR = 0.5 x 4 X 7 = 14 sq cm.
Area of the Triangle ODQ = 0.5 x OD x DQ = 0.5 x 3 x 5 = 7.5 sq cm.
Area of the Triangle POQ = 0.5 x PO x OQ
PO = SO/2.
SO = √(AO² + AS²) = √(7² + 6²) ≅ 9.2195
PO ≅ 9.2195/2 ≅ 4.6097
OQ = √(DO² + DQ²) = √(3² + 5²) ≅ 5.8309
Therefore, Area of the Triangle POQ = 0.5 x 4.6097 x 5.8309
= 13.4395 sq cm.
Area of the quadrilateral PQRS = 100 - (13.4395 + 21 + 7.5 + 7.5 + 14)
= 36.5604 sq cm.
1.7% or ₹ 150.00/- whichever is higher of an employee’s salary is paid as professional tax per month and 22% of the balance per year as income tax where first ₹ 45,000.00/- is tax free. If employee’s salary is ₹ 8,500.00/- per month, how much amount does he pay per year as income tax?
Options:
Option (a): ₹ 10,144.00 /-.
Option (b): ₹ 11,120.00 /-.
Option (c): ₹ 10,256.00 /-.
Option (d): ₹ 12,144.00 /-.
Total annual salary = ₹ 8,500.00 x 12 = ₹ 1,02,000.00/-
1.7% of ₹ 8,500.00 = ₹ 144.50/-
So, professional tax per month = ₹ 150.00/-
Therefore, total professional tax = ₹ 150.00 x 12 = ₹ 1,800.00/-
Salary after professional tax deduction = ₹ 1,00,200.00/-
First ₹ 45,000.00/- in tax free, so, the taxable income
= ₹ 1,00,200.00 – ₹ 45,000.00 = ₹ 55,200.00/-
Therefore,
Payable income tax = 22% of ₹ 55,200.00/-
= ₹ 12,144.00/-
3/4th of the work can be done Mallika in 15 days. After 10 days, Rani joins her and both work together for 5 days, after which Mallika leaves. If Rani takes 9 more days to complete the work, then, how many days will Rani alone take to do it?
Mallika can complete 3/4 of the work in 15 days. Thus, the total work W can be defined as:
Work done by Mallika in 15 days = (3/4)W
To find her work rate per day:
Work rate of Mallika = (3/4)W / 15 = (3W / 60) = (W / 20)
So, Mallika can complete 1/20 of the work in one day.
In 10 days, the work done by Mallika is:
Work done by Mallika in 10 days = 10 * (W / 20) = (10W / 20) = (W / 2)
After Mallika has worked for 10 days, the remaining work is:
Remaining work = W - (W / 2) = (W / 2)
Let Rani’s work rate be r (the fraction of work Rani can complete in one day).
When Rani joins Mallika, they work together for 5 days. The work done by both in 5 days is:
Work done by Mallika in 5 days = 5 * (W / 20) = (5W / 20) = (W / 4)
The work done by Rani in 5 days is:
Work done by Rani in 5 days = 5r
Thus, the total work done by both in 5 days is:
Total work done = (W / 4) + 5r
Setting the total work done equal to the remaining work:
(W / 2) + ((W / 4) + 5r) = W
Now we simplify this equation:
(W / 2) + (W / 4) + 5r = W
Convert (W / 2) to quarters:
(2W / 4) + (W / 4) + 5r = W
(3W / 4) + 5r = W
Subtract (3W / 4) from both sides:
5r = W - (3W / 4) = (W / 4)
r = (W / 20)
From the calculations, Rani can complete 1/20 of the work in one day. After Mallika leaves, Rani takes 9 more days to complete the remaining work.
The remaining work after the 15 days of work is:
Remaining work = (W / 2) - ((W / 4) + 5r) = (W / 2) - (3W / 4) = (W / 4)
We know Rani takes 9 days to finish the remaining (W / 4):
Work done by Rani in 9 days = 9 * r = 9 * (W / 20) = (9W / 20)
To find how many days Rani alone would take to complete the entire work W, we use:
Days for Rani to complete W = W / r = W / (W / 20) = 20 days
Thus, Rani alone will take 20 days to complete the work.
Read the directions given below and solve the questions based on it.
Mark (A): If the question can be answered by using one of the statements, but cannot be answered by using other statement.
Mark (B): If the question can be answered by using either statement alone.
Mark (C): If the question can be answered by using both statements together, but cannot be answered by using either statement alone.
Mark (D): If the question cannot be answered even by using both the statements together.
The one of the base angle of a triangle is 45° and base is 120 cm. What is the length of the shortest side of the triangle?
Statement A: The sum of the lengths of the other two sides is 160 cm.
Statement B: The other base angle is 60°.
Options:
Option (a): A.
Option (b): B.
Option (c): C.
Option (d): D.
Consider Statement A: The sum of the lengths of the other two sides is 160 cm.
Let the triangle be ABC, with
AB=120,
BC=a,
CA=b=160−a,
∠B=60°.
Let CD be the altitude to AB.
Let x = BD.
∴CD= √3 x, a=2x, b=160−2x;
∴3x²+(120−x)²=(160−2x)²;
3x² + x² – 240x + 14,400 = 25,600 – 640x + 4x²
∴400x= 11,200; => x = 140 and
∴a=28 x 2 = 56,
∴b=104.
Consider Statement B: The other base angle is 60°.
Since two given angles are 45° and 60°, third angle is 180° - (60° + 45°) = 75 °
So, adjacent side of 60° will be the shortest because opposite side of the largest angle will be the shortest.
Question can be solved by using either of the statement alone. Hence option (B) is the answer.
Read the directions given below and solve the questions based on it.
Mark (A): If the question can be answered by using one of the statements, but cannot be answered by using other statement.
Mark (B): If the question can be answered by using either statement alone.
Mark (C): If the question can be answered by using both statements together, but cannot be answered by using either statement alone.
Mark (D): If the question cannot be answered even by using both the statements together.
A, B, C, D, & E are five integers such that E < D, C > E, A < C < B. Is A the smallest integer?
Statement A: E + B < A + D
Statement B: B < D
Options:
Option (a): A.
Option (b): B.
Option (c): C.
Option (d): D.
Let us consider: E < D, C > E, A < C < B
According to the above statement, A < E < C < B and E < D
Consider Statement A: E + B < A + D
Can’t determine whether, A will be the smallest integer.
Now Consider Statement B: B < D
So, A < E < C < B < D
Therefore, A will be the smallest integer.
Hence answer option is (A).
Read the directions given below and solve the questions based on it.
Mark (A): If the question can be answered by using one of the statements, but cannot be answered by using other statement.
Mark (B): If the question can be answered by using either statement alone.
Mark (C): If the question can be answered by using both statements together, but cannot be answered by using either statement alone.
Mark (D): If the question cannot be answered even by using both the statements together.
If w, x, y, and z are the digits of the four-digit number N, a positive integer, Is the number N divisible by 5 with remainder 0?
Statement A: w + x + y + z = 17
Statement B: N + 5 is divisible by 5
Options:
Option (a): A.
Option (b): B.
Option (c): C.
Option (d): D.
Consider Statement A: w + x + y + z = 17
Can’t determine remainder when N is divided by 5.
Now Consider Statement B: N + 5 is divisible by 5
Hence answer option is (A).
Instead of 42 a candidate took 24 as divisor. Which gives a quotient of 49. Find the correct quotient.
Note: remainder is 0.
Options:
Option (a): 25
Option (b): 26
Option (c): 29
Option (d): 28
The Remainder theorem we have is
Number = Quotient x Divisor + Remainder
Here remainder = 0
So, Number = Quotient x Divisor
number = 49 x 24
number = 1176
Now, the divisor was wrongly taken as 24 instead of 42
So, for correct divisor we have
1176 = Quotient x 42
Quotient = 1176 / 42
Quotient = 28
The correct quotient is 28.
A certain sum is lent out at a certain rate of interest for a certain period and the amount is 3.4 times as the principle. Had it been lent out on 64% higher rate of interest for 44% less time period the amount would have been how many times the principle?
Options:
Option (a): 2.75 times.
Option (b): 3.5 times.
Option (c): 3.7 times.
Option (d): 3.2 times.
Let the principal = P,
the interest rate = r
and the time period = t
Amount = 3.4 P. Therefore the interest = 3.4P - P = 2.4P
SI = P*r*t/100
2.4P = P*r*t/100
rt/100 = 2.4
New Rate = 64% more = 1.64r
New Time = 44% less = 0.56t
SI = P * 1.64r * 0.56t/100 = 0.9184P * rt/100 = 0.9184P * 2.4 = 2.20416P
The final amount = P + SI = P + 2.20416P = 3.20416P = approx 3.2 times
Hence answer option is (D).
The areas of the three adjacent faces of a rectangular (▢le) box which meet in a point are known. The product of these areas is equal to:
Options:
Option (a): The volume of the box.
Option (b): Twice the volume of the box.
Option (c): The square of the volume of the box.
Option (d): The cube root of the volume of the box.
Let length = l, breadth = b and height = h. Then,
Product of areas of 3 adjacent faces = (lb*bh*lh) = (lbh)²
= (Volume)²
Hence option (C) is the answer.
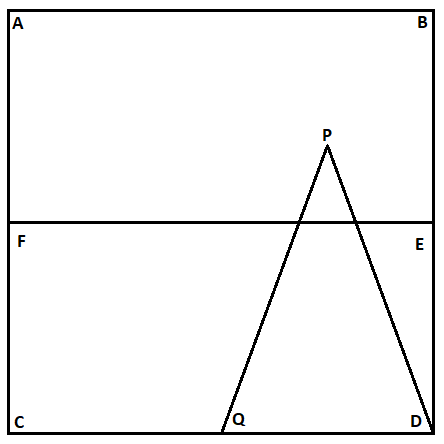
ABCD ia a square (▢re) with area 16 sq units. E, F and Q are the mid points of BD, AC and CD respectively. If P is any point inside the rectangle (▢le) ABEF and if X is the area of the triangle (▲le) DPQ, then choose the options that is true?
Options:
Option (a): 2 < x < 4.
Option (b): 8 < x < 32.
Option (c): 16 < x < 32.
Option (d): 16 < x < 64.
Given DE = 2 units.
Let PQ be the altitude of the triangle (▲le) DPE
2 < PQ < 4
-> ½ x 2 x 2 < Area of ▲le DPE < ½ x 2 x 4
-> 2 < Area < 4.
Hence option (A) is the answer.
There are 8 types of chocolates in a shop; in how many ways can a person buy 16 chocolates?
Options:
Option (a): C(12, 8).
Option (b): C(23, 7).
Option (c): C(22, 7).
Option (d): C(24, 7).
The required number of ways is the number of non-negative integral solution of
A1 + A2 + ……. A8 = 16
Therefore, number of ways is (16 + 8 - 1)C(8 – 1) = ₂₃C₇ = C(23, 7)
Hence answer option is (B).
Let S = 1/3 + 1/(3)² + + ……….; then (0.25)^(log₂ S) is ?
(1/3) / (1 - (1/3)) = ½.
(0.25)^(log₂ S)
= (-0.5)^(-2log₂ 2)
= (0.5)^-2
= 4
In a test, Raja scored 30% of the maximum number of marks and fails by 40 marks, but Sundar candidate who scores 45% of the maximum number of marks gets 20 marks more than necessarily passing marks. What is the maximum mark in the test?
Let maximum marks is X. According to the question,
30% of X + 40 = 45% of X – 20.
Solving this, we get, X = 400.
X is a number formed by writing the first 1002 whole numbers one after another from left to right then a vertical line is drawn which divides the number such that the number of digits on either side of line is the same. Find the remainder when the number by the digits on the left of vertical line, is divided by 25
Options:
Option (a): 5.
Option (b): 3.
Option (c): 2.
Option (d): 4.
0 to 9 - 10 digits,
10 to 99 - 90 x 2 = 180 digits,
100 to 999 - 900 x 3 = 2700 digits,
and 1000 and 1001 - 8 digits.
Total 10 + 180 + 2700 + 8 = 2898,
2898 / 2 = 1449,
1449 - 190 = 1259,
1259 / 3 = quotient 419 with remainder 2,
419 + 100 = 519 two more digits = 51952,
last 2 digits 52, Now apply divisibility rule for 25,
remainder 2. (divisibility rule for 25 - consider last 2 digits.)
If a = 2019, b = 2020 and c = 2022, then find the value of a² + b² + c² – 3abc.
a³ + b³ + c³ – 3abc
= ½(a + b + c)[(a – b)² + (b – c)² + (c – a)²]
= ½(2019 + 2020 + 2022)[(2019 – 2020) ² + (2020 – 2022) ² + (2022 – 2019)²]
= 42,427.
Natural numbers are written in the shape as shown below. Find the sum of all the numbers in the 100th row?
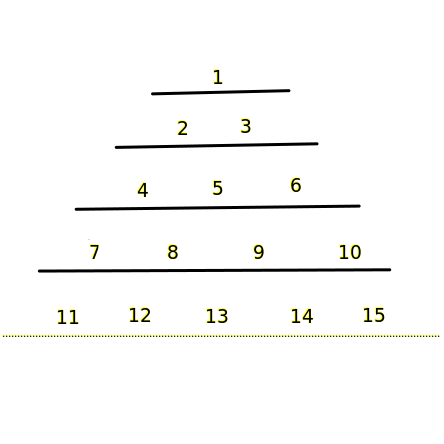
We can write numbers of the above pyramid in the form,
(n(n²+1))/2
Now put n = 100 to find the sum of the 100th row.
= (100(100 ² + 1))/2
= 5,00,050
The maximum value of a quadratic function
is 3 when x = 1. Quadratic function’s value at x = 0 is 1. What is the value of the function at x = 5?
Suppose that the quadratic function is f(x) =ax² + bx + c.
Also, f(0) = 1 implies that c = 1.
As we know that, f(x) attains maximum value at
(α + β) / 2 = -b/2
Or, (α + β) / 2 = 1 implies that (α + β) = -2 implies that b = -2a (only when a<0)
Or, that f(1) = a + b + c = 3 or a = -2 & b = 4
So, f(x) = -2x² + 4x + 1
f(5) = -2(5)² + 4(5) + 1 = - 50 + 20 + 1 = - 29
The surface area of cuboids is 96 cm². Find the maximum volume of the cuboids?
Options:
Option (a): 48 cm³.
Option (b): 64 cm³.
Option (c): 100 cm³.
Option (d): 84 cm³.
The maximum volume is obtain when x, y, and z are equal
— that is, when the cuboid is, in fact, a cube.
A cube has six equal surfaces. 96 ÷ 6 = 16
The area of each surface is 16. Each surface is a square.
The length of each edge is the square root of 16, or 4.
The volume is equal to 4 * 4 * 4 = 64 cm³.
If the roots of the equation x² + px + q = 0 differ from the roots of the equation x² + qx + p = 0 by the same quantity, then what is the value of (p + q)?
Let x1, x2 be the roots of the equation x² + px + q = 0 and x3,
x4 be the roots of the equation x² + qx + p = 0.
Hence,
x1 + x2 = -p,
x1 × x2 = q,
x3 + x4 = -q,
x3 × x4 = p -----(1)
According to the question, x1 – x2 = x3 – x4
or,
(x1 – x2)² = (x3 – x4)²,
or,
(x1 + x2)² – 4 x1×x2
= (x3 + x4)² – 4 x3 × x4 -----(2)
Putting the values from (1) in (2), we obtain (p-q) (p+q+4) = 0
Hence either p = q (not possible otherwise both the equations will become same) or
p + q = -4.
If a, b, c and d are real numbers such that b>0, d>0 and a/b< c/d, then which of the following is true?
Options:
Option (a): a/b < (a-c)/(b+d) < c /d.
Option (b): a/b < (a+c)/(b+d) < c /d.
Option (c): a/b < (a-c)/(b-d) < c /d.
Option (d): a/b < (a+c)/(b-d) < c /d.
a/b < (a+c)/(b+d) < c /d. Is true.
Tops of two poles of height 24m and 16m of are connected by a wire. If the wire makes an angle 45° with the horizontal, then the length of the wire is
Options:
Option (a): 12.01 m.
Option (b): 11.31 m.
Option (c): 13.01 m
Option (d): None of these.
Given that: Heights of two poles are 24 m and 16 m respectively.
Angle wire makes with horizontal = 45°.
Let distance between two poles be x
and length of the wire be y\n tan 45° = (24 – 16)/x = 8 / x
1 = 8 / x
=> x = 8
As length of the wire will form the hypotenuse of right angled triangle, Thus formed,
y² = 8² + 8² = 128
Therefore, y = 11.31 m
Find the present value of the payments received if compound interest of 10% p.a. is reckoned. ₹ 9,240.00/- received at the end of the 1ˢᵗ year and ₹ 7,744.00/- at the end of the 2ⁿᵈ year.
If a sum of Z is received at the end of n years then the present value of that amount is
[z/(1 + (r/₁₀₀))]
Hence, present value of the payments received is
= (9240 /1.1) + (7744/1.21)
= 8400 + 6400 = 14,800.00/-
Page updated in: December 2022
Made with
No Code Website Builder