Option (d): 206
Apply the formula:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C)
n(A ∪ B ∪ C) = a + b + c + d + e + f + g = 1000
n(A) = a + b + d + e = 658
n(B) = b + d + c + f = 372
n(C) = d + e + f + g = 590
n(A ∩ B) = b + d = 166
n(B ∩ C) = d + e = 434
n(C ∩ A) = d + f = 126
1000 = 658 + 372 + 590 - 166 - 434 - 162 + n(A ∩ B ∩ C)
n(A ∩ B ∩ C) = 106
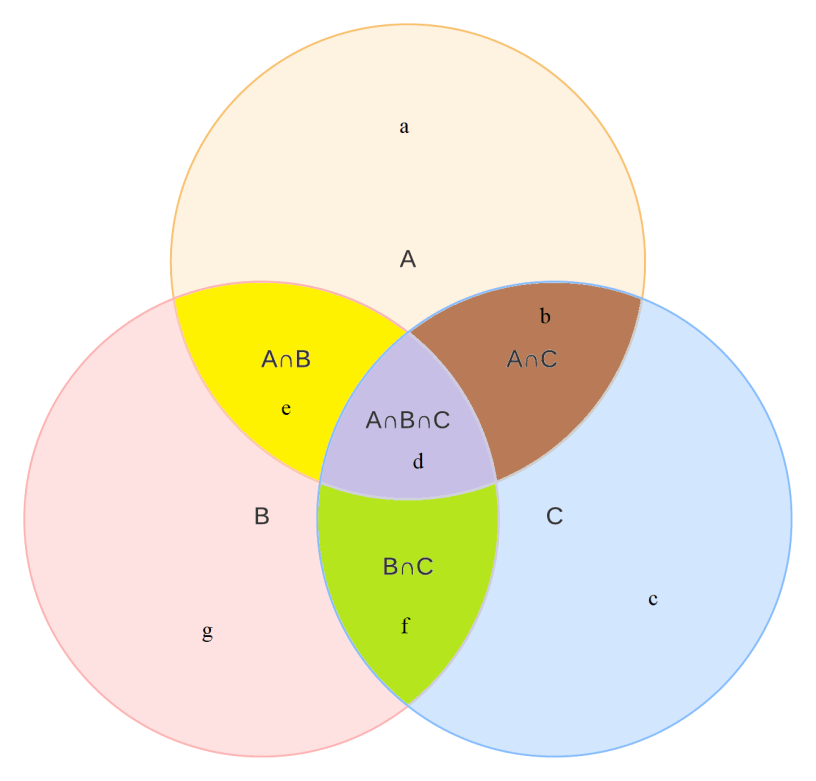
Venn - diagram
From the equations above:
b + c + 126 = 372 => b + c = 246,
434 + f + g = 590 => f + g = 156,
a= 1000 - 246 - 434 - 156 = 164
b = 658 - 434 - 164 = 60
c = 186
d = 106
e = 38
f = 372 - 166 - 186 = 20
g = 136
From Venn-Diagram,
the loss (assuming no profit) suffered by people who purchased shares of brand C but not brand A
= 186 + 20 = 206